통계 입문 – (9) 구간 추정

구간 추정치는 점 추정치에서 오차 한계라고 하는 값을 더하고 빼서 계산합니다.

.

1. 모집단의 표준편차를 알고 있을 때

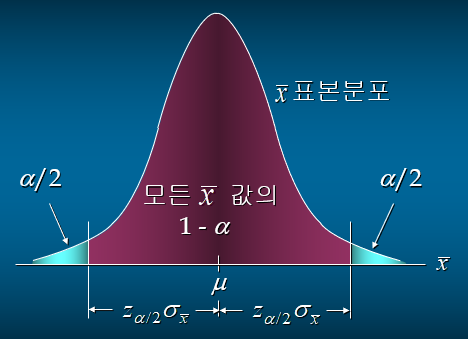
– 대표적인 신뢰 수준에 대한 z 값

.

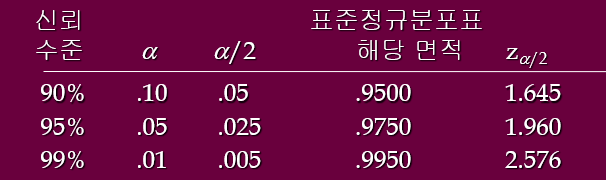
EX) n=36, 표본 평균 소득은 $41,100이고 모집단의 분포는 대략 대칭적입니다.

모집단 표준 편차는 $4,500로 추정됩니다. 간격 추정을 위해

0.95의 신뢰 계수가 사용됩니다.

-> 오차범위 = 1.96*4500/6 = 1,470

즉, $39,630에서 $42,570 사이는 95% 신뢰할 수 있습니다.

신뢰 수준을 높이려면 오차 범위와 신뢰 구간의 폭을 늘려야 합니다.

.

.

2. 모집단의 표준편차를 알 수 없는 경우

샘플의 표준 편차 s는 추정치로 사용됩니다.

이때 표본 평균의 구간 추정치는 t분포를 기준으로 한다.

.

– t 분포

t 분포는 확률 분포의 한 유형입니다.

특정 t-분포는 자유도에 따라 분포가 다릅니다.

자유도가 증가할수록 t-분포의 변동성은 감소합니다.

또한 t분포와 표준정규분포의 차이는 점점 작아진다.

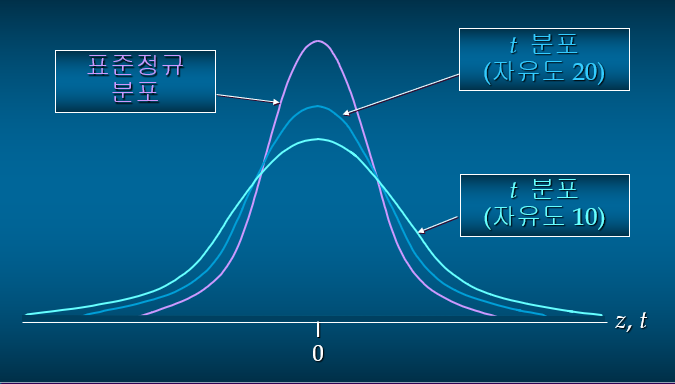
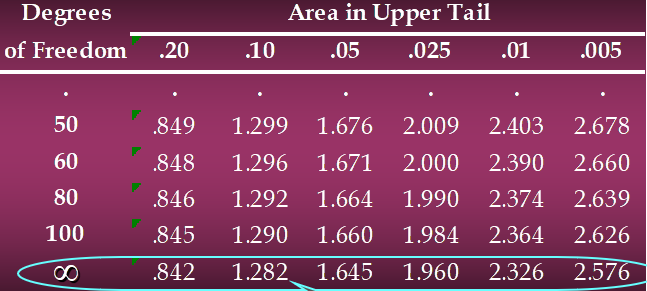
자유도가 100을 초과하면 z-값을 사용하여 t-값을 근사화할 수 있습니다.

z 값은 t-분포표에서 자유도가 무한인 행에서 찾을 수 있습니다.