지금까지 연속 독립 변수를 사용하여 회귀를 수행했습니다. 회귀 분석이 항상 연속적인 독립 변수만 가지는 것은 아니죠? 예를 들어 남성/여성, 계층, 혈액형, MBTI 등. 이러한 변수는 숫자 값이 아니기 때문에 회귀 분석에 사용하기 어렵습니다. – 아니, 그런 것도 돌아간다. 절제가 뭔지 모르겠어… –
이 경우 이제 범주형 변수를 숫자 변수로 변환하여 회귀를 수행할 수 있습니다. 어찌 보면 데이터의 범주가 1과 0으로 늘어나서 특징이 표시된다. 멀게 들리면 예를 들어 다음과 같은 데이터가 있다고 가정해 보겠습니다. 자세히 살펴보십시오.
이 데이터에서 성별과 혈액형은 범주형 데이터입니다. 이해를 돕기 위해 먼저 성별 특성을 더미 변수로 만들어 보겠습니다. 어떻게 보면 남성과 여성의 두 가지 혈액형이 있어야 합니다. 1과 0으로 두 가지 혈액형을 잘 표현하는 특별한 방법이 있나요? 그렇습니다.
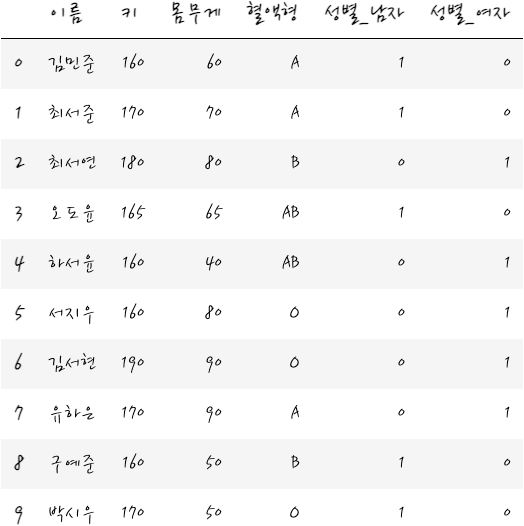
그래서 성별이 남성이면 gender_male만 1이고 나머지는 0이고, 성별이 여성이면 gender_female만 1이고 나머지는 0입니다. 이렇게 놓을 수 있습니다. 마지막으로 이렇게 수치적으로 표현할 수 있기 때문에 회귀분석을 할 수 있습니다. – 참고로 범주형 변수를 1/0 형식으로 만드는 과정을 원 핫 인코딩이라고 합니다. – 이 하나의 핫 인코딩 변수를 더미 변수라고 합니다.
그러나 여기서 고려해야 할 사항이 있습니다. 이렇게 모든 범주를 고려하여 더미 변수를 만들면 어떤 문제가 발생합니까? 그게 무슨 뜻이야
예를 들어, sex_male과 gender_female을 고려하여 회귀를 한다면
$$ y = b_0 + b_{1}x_{남자} + b_{2}x_{여자} $$
이 회귀 방정식을 찾으면 남자와 여자의 관계
$$x_{남자} + x_{여자} = 1$$.
이러한 이유로,
$$ x_{여자} = 1 – x_{남자}$$
그런 관계가 성립합니다.
흠 이제 이것을 원래 회귀 방정식에 대입하면
$$\시작{정렬}
y &= b_0 + b_{1}x_{남자} + b_{2}x_{여자} \\&= b_{0} + b_1(1-x_{여자}) + b_2 x_{여자} \\&= (b_0 + b_1) + (b_2-b_1)x_{여자}
\end{정렬}$$
이렇게 정리되어 있습니다. 이 경우 여성 성별 중 하나로 회귀식을 풀고 원래 분석해야 할 계수가 혼재되어 있어 나누어서 분석할 수 없는 난리가 난다. 당신은 무엇을 볼 수 있습니까? 다중공선성 맞죠? 원래 설명하려 했던 계수를 설명할 수 없는 현상. 최근까지 이것 때문에 많이 고민했는데, 여기서 또 속이 썩고 있습니다. 처분하다.
$$ x_{여자} = 1 – x_{남자}$$
이런 식으로 독립 변수는 서로 선형 관계를 형성해서는 안됩니다. 으흠~ – 더미변수의 다중공선성으로 인해 발생하는 문제를 학술용어로 더미트랩(dummy trap)이라고 합니다. –
그러면 어떻게 해야 합니까?

여자든 아니든 이렇게 1로 나누면 완벽할 것 같다. 0이면 확실히 여자가 아니다. 그래서 남자를 의미합니다. 이렇게 하면 더미 변수로 인한 다중 공선성을 잊을 수 있습니다. 성별이 0이면 문자 그대로 남성으로 해석할 수 있고 1이면 여성으로 해석할 수 있습니다.
그럼 혈액형이 4가지인데 어떻게 하면 될까요?
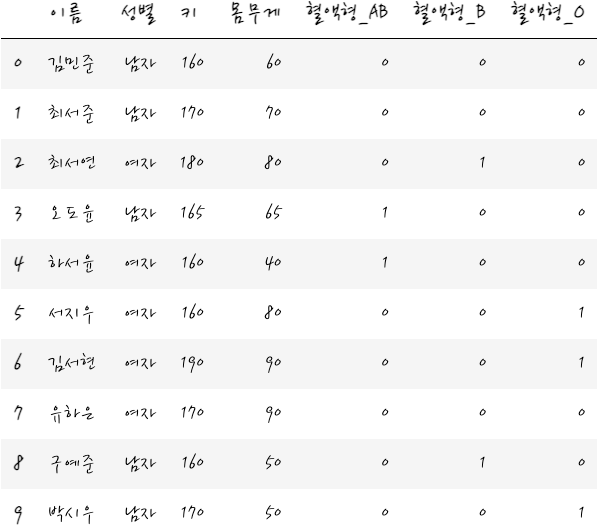
이때 혈액형은 A형을 제외하고 만들 수 있다. 모두 0이면 A입니다.
쉽게 넣어
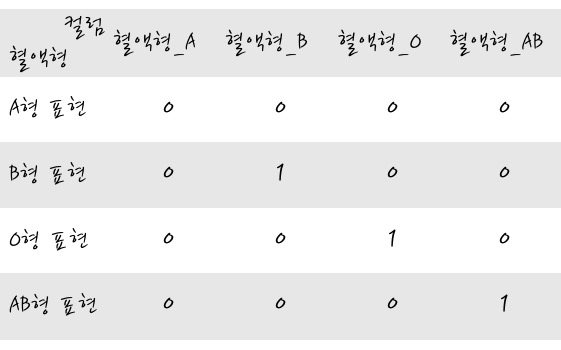
이렇게 될까요? 그런데 제가 다중공선성을 얘기할 때 다중공선성을 설명하는 더미변수를 만들어야 한다고 했는데 그렇다면 그렇게 설정해야 하지 않을까요? 의문이 있을 수 있지만 이렇게 설정하면 값의 크기에 따라 순서가 생성되고 순서가 생성되면 그 크기는 회귀를 수행할 때 의미를 갖게 됩니다. 카테고리는 그런 의미가 아니므로 그런 순서가 없도록 모두 분리합시다. 이런.
결국 더미 변수는 모든 값이 0인 경우를 기준으로 기본 범주를 다른 범주와 비교할 수 있습니다.
이제 범주형 데이터를 더미 변수로 변환하는 방법을 알았으므로 해석에 의한 의미도 알아야 합니다.
가장 중요한 것은 dummy는 범주형 데이터이기 때문에 회귀 방정식의 기울기와는 관련이 없고 y-절편과 관련이 있습니다.
어떻게?

이때 x1이 더미임을 감안하면 x1이 1일 때 x1의 계수 b1과 함께 x1의 영향도 사라지고, x1이 0일 때 x1의 영향도 사라진다. 지금까지 더미변수를 살펴보았는데, 혈액형의 경우처럼 둘 이상이면 그 숫자만큼 y절편이 이동합니다. 그건 매우 쉬워요. 그래서 x1이 성별이라고 생각하면 b1을 통해 남성과 여성의 차이로 해석할 수 있습니다. 이런.
결국 0이 아닌 더미계수에 의해 표준 상태와 차이가 있다고 해석할 수 있다.
이 더미 변수를 만들었으므로 회귀 후 결과를 해석할 수 있어야 합니다. 결과를 해석하기 위해 회귀분석을 많이 했으므로 생략하고 샘플 결과를 예로 들어보겠습니다.
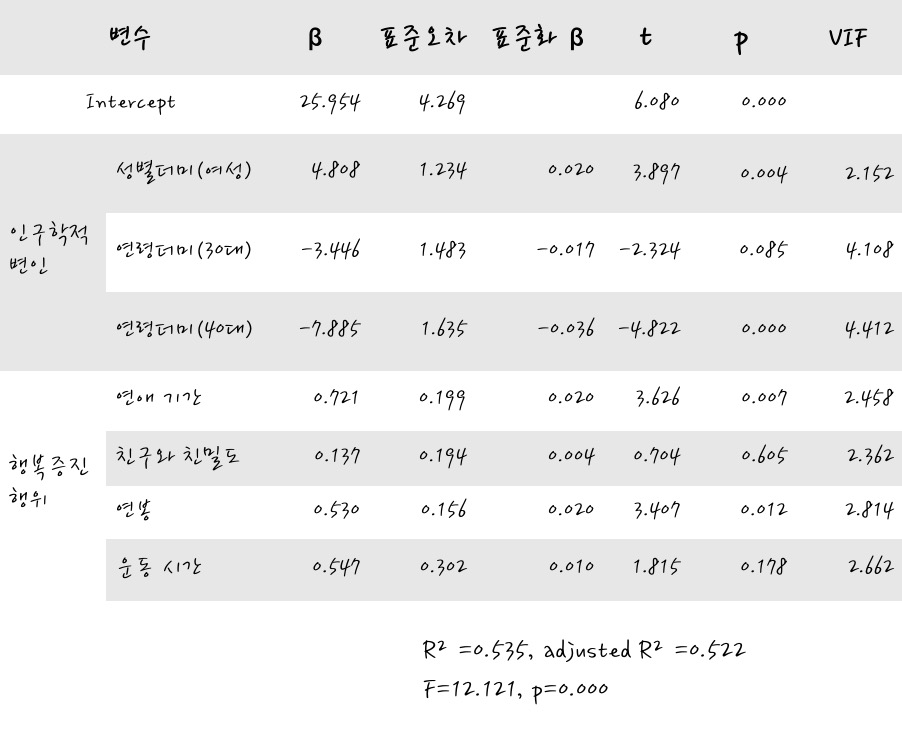
이 회귀분석 결과 종속변수는 행복, 더미나이는 연령, 표준 더미변수는 20대이다.
회귀에 관해서는,
$$\begin{aligned} y_{행복} = b_0 &+ b_1 x_{남자} + b_2 x_{나이30} + b_3 x_{나이40} \\ &+ b_4 x_{데이트} + b_5 x_{친구} + b_6 x_ {급여} + b_7 x_{운동} \end{aligned}$$
회귀의 관점에서 이것을 이해하고 싶습니다. 이제 회귀 결과 분석표를 보고 차근차근 해석해 보세요.
⓵ 결정계수와 보정결정계수가 꽤 높죠? 0.535, 0.522. 회귀 방정식의 중요성은 상당히 높습니다.
⓶ F-검정 결과가 유의하다. F 통계량은 12,121로 상당히 큽니다. 회귀분석 결과 통계적으로 유의미한 결과라고 생각합니다.
⓷ VIF를 보면 문제를 나타낼 만큼 큰 변수가 보이지 않습니다. 나는 너무 행복해. 모델에서 다중 공선성이 발견되지 않았습니다. 다만 참고로 더미변수의 VIF가 크더라도 더미변수가 우리가 분석해야 할 범주형 변수라면 그대로 두고 해석해야 한다.
⓸ 계수의 유의성을 해석할 때 더미(독립)변수는 여성과 30대 연령이었으며, 기타 독립변수로는 연애기간과 연봉이 유의하였다. 하지만 여성과 남성의 행복에는 차이가 있고, 20대(디폴트)와 40대의 행복에는 차이가 있다. 30대의 경우 계수가 유의하지 않으므로 표준 연령인 20세에서 벗어나는 증거가 없다고 상상할 수 있습니다. 그리고 관계 기간과 연봉이 행복에 미치는 영향에 대해 이야기할 수 있습니다.
⓹ 그러면 이 분석 결과를 표준화된 계수와 함께 보면 그 영향을 알 수 있어 상대적인 영향을 잘 설명할 수 있다. 40세 이상은 -0.036으로 큰 부정적 영향을 미쳤고, 여성의 승인 및 데이트 기간은 0.02, 연소득은 0.02로 나타났다. 전반적으로 여자는 여자다, 연애기간과 연봉이 높을수록 행복도가 높다고 해석할 수 있다. 20대들에게.
⓺ 실제 가치 변화를 해석하면 40대 여성이 남성보다 4.808, 40대는 20대보다 7.885 덜 행복했다. 연애 기간이 1단위(1년) 늘어날 때마다 나는 0.721씩 행복해지고 연봉은 1단위(100만원)당 0.530씩 올랐다.
분석 결과는 매우 현실적입니다. 급여가 높을수록 만족도가 높아집니다.
어때? 별거 아니야, 그렇지? ㅋㅋㅋ

참고로 pandas dataframe은 drop_first=True를 추가하고 설정할 때 pd.get_dummies(data=df, column=(‘gender’, ‘blood type’)라는 더미 변수를 자동으로 생성하는 방법을 제공합니다. 첫 번째 값을 0으로 설정하고 전체 카테고리 1의 더미 컬럼을 생성하므로, 첫 번째 삭제만 하지 않고 더미 생성 후 참조 컬럼을 삭제하는 방법을 사용합니다.

지금까지 독립변수가 범주형, 양적변수인 경우를 살펴보았는데, 반대로 종속변수가 더미 범주형 변수라면 어떻게 될지 궁금하다. 예를 들어 어떤 사람이 결혼할 것인지(1) 결혼하지 않을 것인지(0) 결정을 내리려는 경우입니다. 이러한 의사 결정은 임금, 교육 수준, 상대방의 태도와 같은 다양한 양적 변수의 영향을 받습니다. 이 경우 이전과 다르게 소위 로지스틱 회귀를 수행하고 분류 후 연결하기도 합니다. 흥미로운 – 흠 – 다음 이야기 예고편.
